Gradient descent به steepest descent هم معروفه و از این روش جهت پیدا کردن مینیمم یک تابع استفاده میشه. برای محاسبه خطا هم ما یک تابع هزینه یا همون cost function داریم که بعضا در کتب مختلف اسامی متفاوتی دارد و از اون به Performance index هم یاد میشه. حالا برای مینیمم کردن مقدار تابع هزینه (یا تابع خطا) شیوه کار به این صورت هست که ما ابتدا با حدس اولیه ای از جواب کار را شروع میکنیم . سپس گرادیانت تابع را در نقطه ای که پیدا کردیم حساب میکنیم. ما جوابها رو در جهت منفی گرادیانت انتخاب کرده و همینطور ادامه میدیم الگوریتم رفته رفته در نقطه ای که گرادیانت مساوی صفر میشه به جواب میرسه (همگرا میشه) و این همون نقطه مینیمم محلی هست.
اگر دنبال ماکسیمم محلی باشیم از الگوریتم gradient ascent استفاده میکنیم که نزدیکترین ماکسیمم محلی نسبت به جواب فعلی رو با گام برداشتن در جهت مثبت گرادیانت بدست میده. هر دوی این الگوریتمها از مشتق اول توابع استفاده میکنن.
بعنوان مثال فرض کنید ما تابع f(x) ای داریم که میخوایم مینیمم اونو بدست بیاریم .با دادن مقادیری مثل x0 بجای x در تابع فوق ما میتونیم مقادیر اونو تو هر جهت دلخواه تغییر بدیم (با توجه به ابعاد x مثلا اگه x تک بعدی باشه ما میتونیم مقدار شو کم یا زیاد کنیم .) برای اینکه بفهمیم چه مقداری تابع f رو مینیمم میکنه ما ابتدا گرادینات تابع (f∇) را حساب میکنیم (یعنی مشتق تابع را در امتداد تمام بعدهای x حساب میکنیم) .گرادیانت مقدار شیب منحنی رو در نقطه x بما میده و جهت اون هم بسمت افزایش مقدار تابع است. بنابر این ما هم مقدار x را مخالف جهت اون تغییر میدیم تا مقدار تابع کاهش پیدا کنه .
xk+1 = xk−λ∇f(xk)
λ>0 یک عدد کوچیکه که باعث میشه الگوریتم ما پرشهای کوچیکی انجام بده و وجودش باعث پایداری الگوریتم ما میشه. مقدار بهینه اون هم به تابع ما بستگی داره. اگر شرایط پایدار باشد و مقدار λ بهینه انتخاب شود تضمین میشه که
f(xk+1) ≤ f(xk)
بعنوان مثال برای تابع f(x) = x^2 داریم :
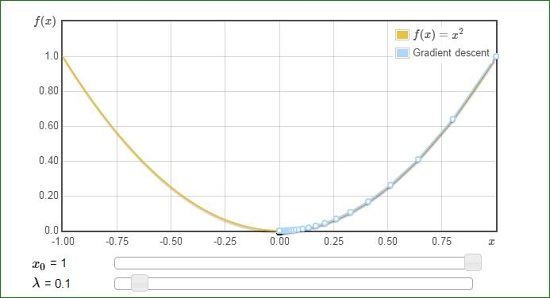
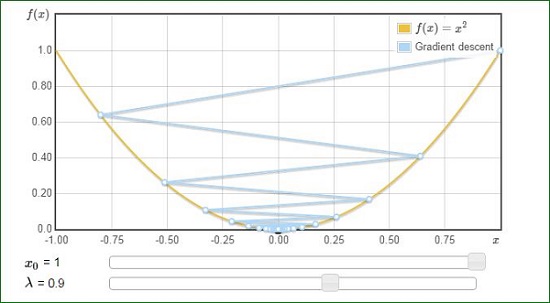
در حالت اول مقدار λ به مقدار بهینه خیلی نزدیکه و در نتیجه سیر رسیدن به جواب مشخص و سیر نزولی داره . اما در نمونه دوم با افزایش مقدار λ شاهد overshooting هستیم که دلیل اون بواسط مقدار بالای λ هست. در این نمونه ما به جواب رسیدیم اما در توابع دیگر با مقادیر بالای λ احتمال diverge کردن هم وجود دارد .