جوابم ممکنه کمی طولانی شه (این نظر من هست بگذارید بقیه دوستان هم نظر بدن) [متاسفانه در قسمت نظرات نمیشه فرمول نویسی کرد:( ]
بیاین مسئله رو به دو بخش تقسیم کنیم: (البته فاکتور های زیادی هست که اینجا اونها رو به حساب نمیاریم و فقط روی صورت مسئله تمرکز میکنیم)
اول اینکه چرا وقتی Relu رو جایگزین توابع فعال سازی مثل Sigmoid و Tanh میکنم مشکل ناپدید شدن در معماری هایی مثل CNN حل میشه؟
دوم اینکه چرا جایگزین کردن تابع فعال ساز Relu با tanh در یک RNN تاثیر مشابهی نداره؟
در یک شبکه کانولوشن معادله هر لایه دقیقا مشابه یک شبکه عصبی سنتی است دلیلش اینه که تصویر ابتدا توسط تابعی مثل img2col تبدیل به فرم ستونی میشه و در نهایت ضرب در قالب دو ماتریس بزرگ انجام میشه.
بگذارید با یه مثال ساده توضیح بدم:
.برای محاسبه این عملیات برای نرون I,j ام در لایه l ما داریم:
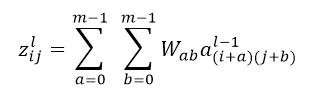
به شکل ساده برای انجام عملیات کانولوشن ، ما بر روی هر عکس ورودی و هر کانال آن به شکل مجزا یک حلقه را اجرا میکنیم و ضرب نقطه ای در هر ناحیه 3*3 را برای هر فیلتر به صورت مجزا اجرا میکنیم که این حلقه بایستی به صورت جداگانه بر روی هر کانال ورودی اجرا شه. اما با توجه به وجود حلقه های متوالی ، این عملیات زمانبره. بدین منظور بایستی عملیات را به صورتی تغییر بدیم که ضرب تمام مکانها به صورت ضرب دو ماتریس در آن واحد اجرا شه. برای سادگی ابتدا عکس ورودی با استفاده از تابعی به نام im2col تبدیل به فرم ستونی میشه. به عنوان مثال در صورتی که توده ورودی ما به شکل 4*4*1*1 (یک عکس با اندازه 4*4 و تعداد یک کانال) و فیلتر مورد نظر ما 2*2*1*1 باشه با استفاده از اندازه گام 1 و پد 1 ما در مجموع 25 محل برای انجام عملیات کانولوشن را داریم:
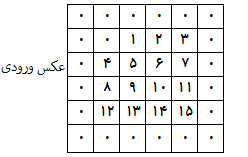
عدد 25 از رابطه زیر بدست میآید:
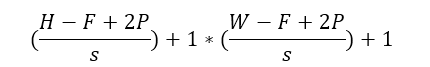
که H,W اندازه عکس ورودی،S اندازه گام، F اندازه فیلتر و P اندازه پد هست.
به عنوان مثال 4 موقعیت اول به شکل زیر هستند:
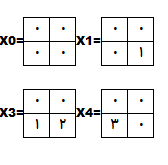
برای همه 25 محل ما یک فیلتر 2*2*1 داریم که به صورت یک ستون 1*4 نوشته میشن.با توجه به اینکه 25 بردار ستونی وجو دارد مارتریس ورودی به شکل 25*4 در میآید .
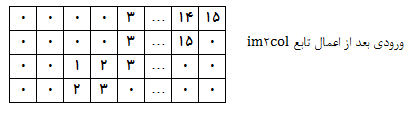
به شکل مشابه وزن ها (فیلتر ها) به شکل ستونی تبدیل میشوند که نتیجه عملیات انتشار رو به جلو برای عملیات کانولوشن در هر لایه ضرب دو این دو ماتریس است
با توجه به مواردی که در بالا گفتم در لایه اول یک شبکه کانولوشن پارامتر های ما W1 و b1 ، در لایه دوم W2 و b2 و به همین ترتیب در لایه های بعد هستند . فرض کنید تابعی که عملیات غیر خطی رو بر روی تابع بالا اعمال میکنه f باشه و خروجی این تابع رو fi (i ایندکس خروجی لایه i ام هست) نام گذاری کنیم.(همچنین فرض کنید که نتیجه عملیات قبل از اعمال تابع فعال ساز در ai ذخیره میشه)
با توجه به تعاریف بالا در یک شبکه کانولوشن با ورودی x خروجی لایه اول به صورت
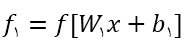
خواهد بود.به همین ترتیب خروجی لایه دوم
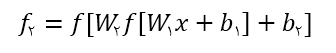
و خروجی لایه سوم
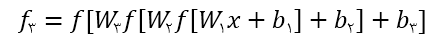
خواهد بود و تابع هزینه L هست.
حالا فرض کنید در طول اجرای الگوریتم backprop میخواهیم مشتق تابع هزینه با توجه w1 رو محاسبه کنیم:
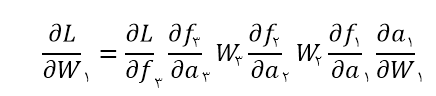
مشکلی که عموما در معادله بالا وجود داره ناپدید شدن گرادیان هست. در معادله بالا مقصرین اصلی که باعث میشن این پدیده رخ بده
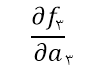
و

هستند!
در تابعی مثل sigmoid بازه مشتق بین (0,0.25] هستش به این معنی که مشتق

و

هست.همونطور که در بالا ذکر شد این مقدار کمتر از 1 هست که در یکدیگر ضرب میشن. حالا فرض کنید که 10 تا لایه داریم در نتیجه مقدار خطایی که با لایه اول میرسه

خواهد بود! (این یعنی ناپدید شدن گرادیان)
این سناریو برای تابع فعال ساز Relu متفاوت هست.در این تابع گرادیان توابع بالا

خواهند بود. مشتق این تابع همیشه 1 هست این یعنی خطای ما در عدد 1 ضرب میشه در نتیجه اون اتفاقی که در تابع sigmoid رخ داد اینجا وجود نداره.
حالا بریم سراغ سوال دوم ، چرا با همه این تفاسیر ، این متد نمیتونه مشکل ناپدید شدن گرادیان رو در یه RNN حل کنه؟
در حقیقت آقای جفری هینتون در مقاله (A Simple Way to Initialize Recurrent Networks of Rectified Linear Units) به وضوح گفتند :

یعنی استفاده از تابع فعال ساز Relu در شبکه های RNN باعث میشه که مقادیر خروجی خیلی بزرگ شن.
اینکه منظورشون از این جمله چیه رو بیاین با معادله RNN نشون بدیم: (در معادله زیر فرض رو بر این میگذارم که با علائم آشنایی دارید و اینکه یک RNN چگونه کار میکنه)

در یک RNN ورودی هر لایه در هر گام xi هست، تفاوت اساسی که RNN با CNN داره، اینه که در یک شبکه کانولوشن در هر لایه پارامتر Wi جدا از هم هستند اما در یک RNN پارامتر W بین تمامی گام ها به اشتراک گذاشته میشه.
فرض کنید از یک گام زمانی خاص شروع کنیم و مقدار bi رو برای سادگی صفر در نظر بگیریم، اتفاقی که میفته معادله زیر هست:

که یه جورایی به ضرب زنجیره ای W اشاره داره.
همنطور که نشون داده شده تا زمانی که مقدار W از یک بزرگتره بعد از چندین بار اجرای عملیات ضرب نتیجه، یک ماتریس با مقادیر بزرگ خواد بود.از سوی دیگر استفاده از Relu به جای sigmoid یا tanh مشکل تحویل گرادیان به لایه های ابتدایی رو نیز حل نمیکنه. در بالا گفته شد که در یک CNN پارامتر های هر لایه W1,W2,W3,… از یکدیگر مستقل هستند، اما در RNN یک ماتریس واحد W در تمامی گام های زمانی دخیل هست . فرض کنید بخواهیم مشتق f3 به W رو محاسبه کنیم، نتیجه به صورت زیر خواهد بود:

اگه به قسمت آخر رابطه بالا توجه کنید

در صورتی که از تابع Relu استفاده شه نتیجه مشتق به صورت زیر خواهد بود:

اما مشکل ما وجود بیش از یک W در رابطه هست.در یک شبکه RNN با افزایش تعداد لایه ها تعداد این W ها نیز افزایش پیدا میکنه که در یکدیگر ضرب میشن.در CNN این پارامتر ها W1,W2,W3,… هستند که جدای اینکه از یکدیگر مستقل هستند اسپارس هم هستند. این خصوصیات تاثیر مستقیم بر روی عدم منفجر شدن گرادیان(gradient explosion) دارند.
و اما برگردیم به IndRNN:
چند هفته پیش ، نوع جدیدی از شبکه عصبی بازگشتی با نام IndRNN توسط Shuai Li ارائه شده که نتایج ارایه شده قابل توجه هستند.این معماری نه تنها مشکل انفجار/ناپدید شدن گرادیان در RNN های سنتی بلکه مشکل یادگیری وابستگی بلند مدت در RNN سنتی رو نیز حل میکنه. فرمول RNN رایج:

(نویسندگان مقاله در این شبکه idnRNN از ضرب هادامارد (درایه ای ) استفاده می کنن به این معنی است که هر نورون یک وزن مجزا داره که به آخرین حالت پنهان آن متصل هست. ضرب هادامارد دو ماتریس A و B را به صورت A o B نمایش داده میشه . تغییر عمده -> (u o ht−1)
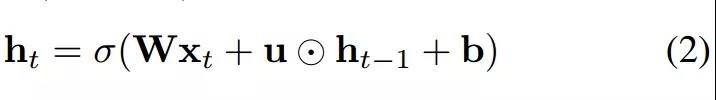
به علاوه از توابع غیر اشباع پذیر مانند relu استفاده شده، این امر باعث شد شبکه بعد از آموزش نسبت به داده های آموزش مقاوم تر شه , همچنین میتوان شبکه های خیلی عمیق تر از RNN های موجود رو با قرار چندین لایه IndRNNs بسازیم. نتایج بدست اومده نشان می ده که استفاده از IndRNN می تواند نتایج بهتری در کارهای مختلف نسبت به RNN سنتی و LSTM و GRU به دست آورد.
